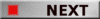DOUBLE STAR NOTES :
RESOLUTION & MAGNITUDE LIMITS
NOTE: This Section Still Requires Expanding!!!
INTRODUCTION : PRECEPTS of RESOULTION
Close Pairs
1) Resolving the closest pairs below about 1 or
2 arcsec can require the combination of aperture, moderate to
high magnification and good seeing. This is also around the
threshold of moderate seeing, meaning that in unfavourable
conditions, these pairs may not be clearly split.
2) For the closest pairs, resolution is assumes
a number of provisos being meet. These include;
a. Both stars are equally 6.0v (visual)
magnitude.
b. Both stars are solar-like yellow stars
c. Aperture is large enough to split the pair
cleanly.
d. Optics are clean, freshly coated if reflectors, and
have optical qualities better than about 1/8th wave.
3) Close pairs which are brighter than
6th magnitude become more difficult to resolve because of the
overwhelming light of the components. This often requires either
the light be reduced via an aperture stop — limiting the
telescopes aperture or using neutral density filters.
4) Close pairs which are fainter in
magnitude are also more difficult to resolve, and are much more
problematic when nearing the faintest magnitude limit of the
telescope.
5) Close pairs with increasing differences in
magnitude (Δm) also become far
more difficult to resolve, as the light of the primary star
often overwhelms the nearby companion. For each magnitude in
difference rises almost exponentially, roughly doubling in
resolution for every two magnitudes.
6) Close pairs have commonly a transition phase
from an apparent single star to seeing the pair cleanly
resolved. As all stars through telescopes are not real pinpoints
but are seen as Airy Disks — a central bright spot
encircled by a number of much fainter rings — the two
stars can appear elongated, joined or merged together. Clean
separation is defined by dark space existing between the
components.
7) Close pairs on the Dawes Limit, may or may
not be cleanly resolved. The empirical Dawes Limit is a result
of a large sample of various sizes of telescopes, each being
tested for their ability to split pairs by average observers
through the Earth’s atmosphere. It
is defined by the simple equation;
Res (arcsec) = 11.58 / D (cm) or
Res (arcsec) = 4.54 / D (inches)
Where;
Res = Resolution in arcsec
D = Aperture in either centimetres or inches.
I.e. 7.5cm (3-inch) is 1.52 arcsec, 10.5cm (4-inch)
is 1.14 arcsec, 20cm (8-inch) is 0.57 arcsec, while 30cm (12.5-inch)
is limited to 0.38 arcsec. 8) Resolution of
Close Pairs also has the Theoretical Limit. This is based on
the criteria from optical theory, and is made on the diameter of the
third outer ring of the observed Airy disk. This limit is 20.9%
bigger than the resolution of the Dawes Limit. I.e. 20cm sees 0.57
arcsec, but the Airy disk covers more like 0.69 arcsec. It is
unlikely that an observer — regardless of the observing
conditions — could exceed this limit. This limit can be
calculated by the simple equation;
TRes (arcsec) = 13.84 / A (cm) or
TRes (arcsec) = 5.43 / A (inches)
Where;
TRes = Theoretical Resolution is in arcsec
D = Aperture in either centimetres or inches.
I.e. 7.5cm (3-inch) is 1.84 arcsec, 10.5cm (4-inch) is
1.31 arcsec, 20cm (8-inch) is 0.69 arcsec, while 30cm (12.5-inch) is
limited to 0.46 arcsec
Standard Pairs
1) All standard pairs (and wider pairs) usually
are easy to resolve regardless of the conditions. Resolution is
not necessarily limited by the atmospheric seeing, and these can
be typically resolved using optimum telescope magnifications
— sometimes called moderate magnifications.
2) Resolution of all standard pairs can be
achieved in small telescopes but usually not so in
binoculars
3) Problems may occur with very bright stars or
those having significant differences in magnitude.
Wide Pairs
1) Wide pairs (and wider pairs) usually are
always easy to resolve regardless of the conditions. Resolution
is not limited at all by seeing, and these can be resolved using
low telescope magnifications.
2) If both stars are viewed in dark skies and
above about 10th magnitude, wide pairs are readily visible in
binoculars. In city skies this may be limited to about 7th
magnitude.
3) Most wide pairs are generally more
spectacular in low magnifications because they can include the
general field stars — especially when they reside in
places in the Milky Way.
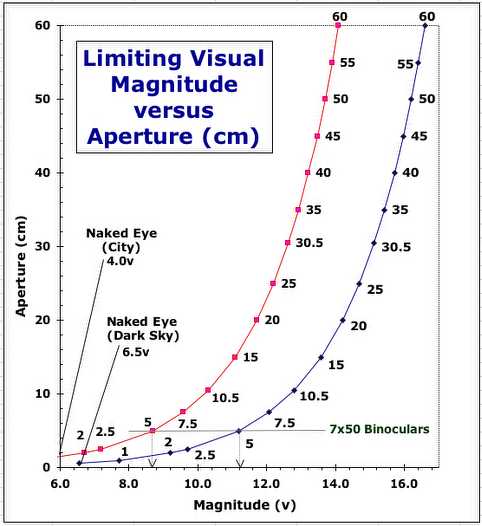
MAGNITUDE LIMITS
1) The other observational constraint on
observing stars is the theoretical magnitude visible for the
aperture used.
2) Magnitude limits or limiting magnitude
are difficult quantities to ascertain because of many other
influencing factors. This includes things such as the observing
conditions (transparency), light pollution, the observer’s eyesight, magnification or
atmospheric seeing.
3) Based on the average observer, a practical
simple calculation is based on either Observed or Theoretical
magnitudes;
m(v) = 2.7 + 5× log ( D (cm) / 10 )
Where;
m(v) = Observed Magnitude Limit.
D = Aperture in centimetres.
Where;
m(v) = Observed Magnitude Limit.
D = Aperture in centimetres
Aperture
(cm.) |
Limit
Mag (v.) |
| 5 | 12.7 |
| 7.5 | 13.1 |
| 10.5 | 13.6 |
| 20 | 14.0 |
| 25 | 14.3 |
| 30 | 14.8 |
| 40 | 15.1 |
| 50 | 15.4 |
These determined limits are only a guide. Strong
colours like deep red variables and luminous blue stars can likely
be seen below the stated threshold limit. Colour contrasts for stars
at the lower end of the range is likely to disappear at these
particular lower magnitudes. Furthermore seeing and transparency
conditions, dust or smoke, and proximity to urban skies through
light pollution can drastically change the telescope magnitude
limits. On the best nights, it is probably possible to get 0.5
magnitudes lower than the limit. It is also quite possible that with
experience and tricks like averted vision may extend these to lower
limits.
Observations and assumptions from which the table was
constructed may be inapplicable to other conditions.;
1) Atmospheric seeing can render small
instruments able to see fainter objects than larger ones.
2) Most telescopes and all observers are not ‘normal’
3) Magnification and eyepiece type will affect the outcome.
4) Direct or averted vision
5) Type of telescope (loss of light in 2-degree spectrum)
6) Bright field objects affect dark adaptation
Last Update : 20th September 2016
Southern Astronomical Delights ©
(2011)
For any problems with this Website or Document please
e-mail me.
|